发表更新 特兹卡特(Tezcat) 翻译 / 伪随机数 / Unity / C#39 分钟读完 (大约5825个字)0次访问

伪随机算法系列-04 Perlin Noise(Gradient Noise)

翻译—-Pseudorandom Noise-Perlin Noise
如果你觉得这篇教程不错,请去支持原作者

此教程使用的Unity版本为2020.3.6f1

  • 制作一个泛型化的晶格(lattice)噪声
  • 添加对梯度噪声的支持
  • 生成1D,2D,3D的柏林噪音

这是伪随机噪音系列教程的第四篇.通过增强值噪音的功能来支持柏林噪声.

3D柏林噪音球体

1 泛型梯度噪声(Generic Gradient Noise)

值噪声是一种在晶格点上定义了恒定值的晶格噪声.通过对这些点进行插值从而产生的一个平滑的图案,但是晶格的样子还是非常明显.另一种方法是在函数之间插值,而不是在常量之间插值.这意味着每个晶格点都有自己的函数.为了保持简单和一致,所有的点都要使用同一个函数计算,只是参数不同而已.最简单的函数是常量值,也就是ValueNoise.再往上一步,就是一个线性依赖于采样点坐标并相对于晶格点的函数.最直接的是$f(x)=x$,x为相对坐标.这将产生以格点为中心的线性坡道或梯度.因此,这种类型的噪声被称为梯度(Gradient)噪声.

因为值噪声是梯度噪声的其中一小种.所以我们可以调整一下晶格噪声的代码使它始终生成梯度噪声.

1.1 梯度类接口(Gradient Interface)

首先为Noise添加一个局部类,命名为Noise.Gradient,在其中定义一个IGradient接口.

1
2
3
4
5
6
7
8
using Unity.Mathematics;

using static Unity.Mathematics.math;

public static partial class Noise
{
	public interface IGradient {}
}

梯度算法的目的是对一个hash值和一个相对坐标进行评估.在接口中定义一个向量化的Evaluate,现在只用于1D噪声,除了传入hash值之外,它还需要X坐标作为参数.

1
2
3
4
public interface IGradient
{
	float4 Evaluate(SmallXXHash4 hash, float4 x);
}

我们像以前做1D值噪声那样添加一个Value结构体,现在只需要它返回hash.Floats01A的值.

1
2
3
4
public struct Value : IGradient
{
	public float4 Evaluate(SmallXXHash4 hash, float4 x) => hash.Floats01A;
}

为了增加对2D和3D噪声的支持,添加另外两个接口.

1
2
3
4
5
6
7
8
public interface IGradient
{
	float4 Evaluate(SmallXXHash4 hash, float4 x);

	float4 Evaluate(SmallXXHash4 hash, float4 x, float4 y);

	float4 Evaluate(SmallXXHash4 hash, float4 x, float4 y, float4 z);
}

Value也必须实现这些方法,依然是简单地返回hash.Floats01A而忽略坐标参数.未使用的参数不会影响性能,因为Burst会优化掉它.

1
2
3
4
5
6
7
8
public struct Value : IGradient
{
	public float4 Evaluate(SmallXXHash4 hash, float4 x) => hash.Floats01A;

	public float4 Evaluate(SmallXXHash4 hash, float4 x, float4 y) => hash.Floats01A;

	public float4 Evaluate(SmallXXHash4 hash, float4 x, float4 y, float4 z) => hash.Floats01A;
}

1.2 梯度输入(Gradient Input)

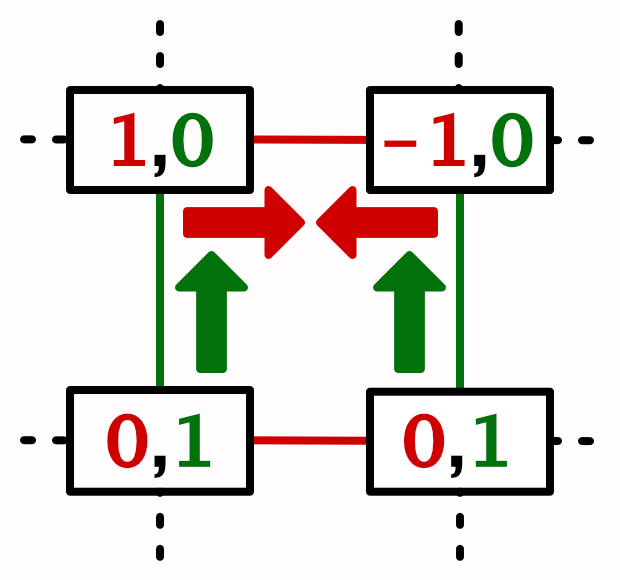
为了向梯度函数提供相对坐标,我们向Noise.Lattice中的LatticeSpan4添加一个向量化的参数g.

1
2
3
4
5
6
struct LatticeSpan4
{
	public int4 p0, p1;
	public float4 g;
	public float4 t;
}

在GetLatticeSpan4函数中,通过使用当前坐标减去p0来得到相对坐标.

1
2
3
span.p0 = (int4)points;
span.p1 = span.p0 + 1;
span.g = coordinates - span.p0;

现在我们可以修改一下Lattice1D.GetNoise4里的代码,通过调用Evaluate函数来代替直接计算hash值的函数,将需要的hash值和相对坐标点作为参数传入.

1
2
3
4
5
6
7
8
9
10
public struct Lattice1D : INoise
{
	public float4 GetNoise4(float4x3 positions, SmallXXHash4 hash)
	{
		LatticeSpan4 x = GetLatticeSpan4(positions.c0);

		var g = default(Value);
		return lerp(g.Evaluate(hash.Eat(x.p0), x.g), g.Evaluate(hash.Eat(x.p1), x.g), x.t) * 2f - 1f;
	}
}

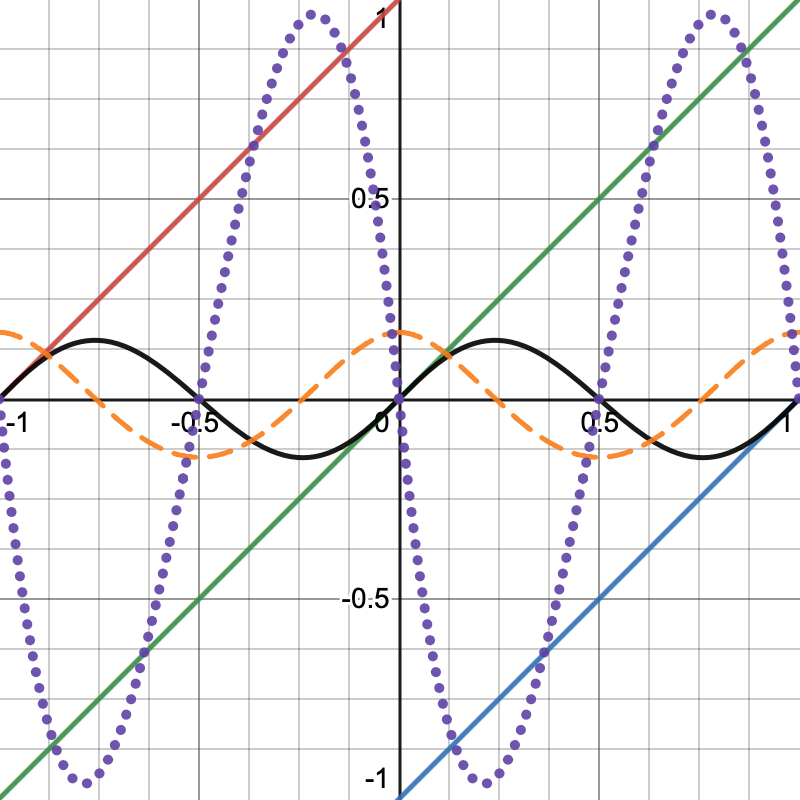
目前我们看到的效果任然和1D值噪声一样,并且连生成的编译后的代码都是一样的.为了理解梯度噪声是如何工作的,我们可以暂时改变一下参数值.把Evaluate函数的代码改成最简单的梯度函数$f(x)=x$.

1
public float4 Evaluate(SmallXXHash4 hash, float4 x) => x;

Raw gradient; 1D noise on a plane; resolution 128.

由此产生的是[-1,1]之间的一串线性梯度斜坡效果.因为我们在基于p0点的每个跨度的左右两半(图上表示为红色和白色部分)都使用了相同的算法,所以这些梯度并没有连在一起.为了做出真正的梯度噪声,右半边第二个梯度的算法必须基于坐标点p1.修改一下LatticeSpan4里的代码,将单个的g参数改为g0和g1.

1
2
3
4
5
6
struct LatticeSpan4
{
	public int4 p0, p1;
	public float4 g0, g1;
	public float4 t;
}

因为第二个晶格点所在的位置正好比第一个点远1个单位,所以修改GetLatticeSpan4的代码,使用g0-1来计算g1.

1
2
3
4
span.p0 = (int4)points;
span.p1 = span.p0 + 1;
span.g0 = coordinates - span.p0;
span.g1 = span.g0 - 1f;

修改下Lattice1D.GetNoise4的代码,使用修改后的相对坐标点,p0和g0为一组,p1和g1为一组.

1
return lerp(g.Evaluate(hash.Eat(x.p0), x.g0), g.Evaluate(hash.Eat(x.p1), x.g1), x.t) * 2f - 1f;

梯度的插值效果

如果我们使用线性插值,得到的效果就是平的,因为梯度会相互抵消.不过我们使用了平滑的C2-连续插值,每个梯度都是由它附近的(左右两边)晶格点的计算而来,因此就能得到一个波浪效果.

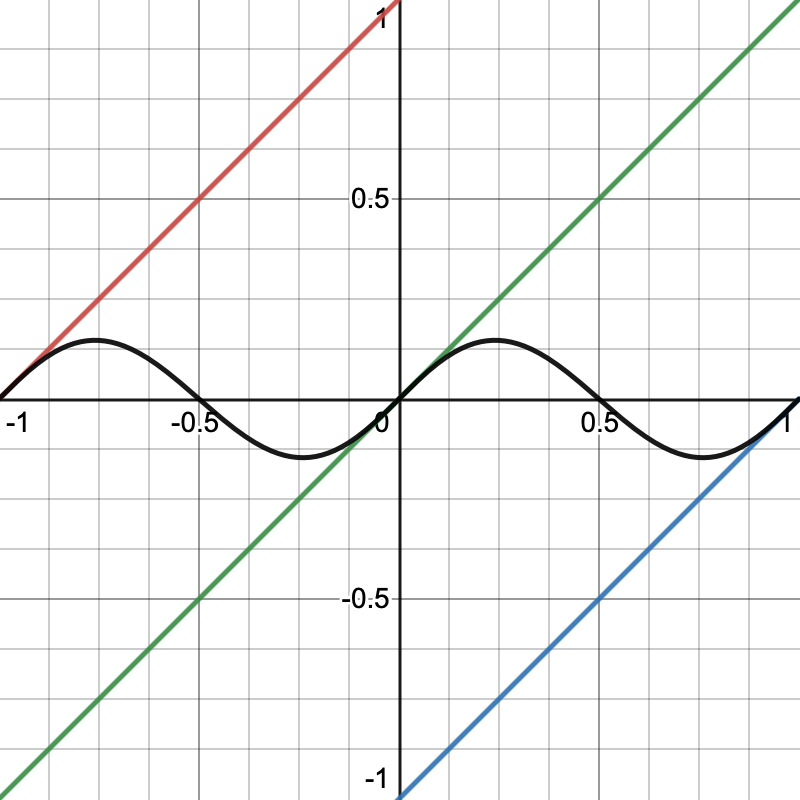
Interpolating three gradients across two spans.

请注意这个梯度效果在晶格点的位置上(-1,0,1)是0,在跨度的中间(0.5)这个插值点的位置也是0,因为梯度值在这几个点的位置上相互抵消了.

现在我们得到的效果是反向的,因为前面我们修改了一下范围.这个修改是当时专门针对值噪音的,所以我们把他改回来,将以前的内容转移到值函数上去.

1
2
3
4
5
6
7
8
9
public struct Value : IGradient
{

	public float4 Evaluate(SmallXXHash4 hash, float4 x) => hash.Floats01A * 2f - 1f;
	
	public float4 Evaluate(SmallXXHash4 hash, float4 x, float4 y) => hash.Floats01A * 2f - 1f;

	public float4 Evaluate(SmallXXHash4 hash, float4 x, float4 y, float4 z) => hash.Floats01A * 2f - 1f;
}

删除掉Lattice.GetNoise1D后的转换.

1
2
return lerp(g.Evaluate(hash.Eat(x.p0), x.g0), g.Evaluate(hash.Eat(x.p1), x.g1), x.t);
	//) * 2f - 1f;
梯度插值函数还是C2连续的吗?

因为梯度函数在晶格点的位置上是斜的,所以一阶导数在此点不再是0,但它在跨度上仍然是连续的,因为两边梯度的波形是重复的.二阶导数在晶格点位置上任然是0,所以是连续的.

Interpolated gradients with 1st and 2nd derivatives, divided by 6 to fit.

1.3 泛型晶格类(Generic Lattice)

现在有了一个梯度值噪声,我们接着做一个Lattice1D的泛型版本,就像Noise.Job那样.

1
2
3
4
5
6
7
8
9
10
public struct Lattice1D<G> : INoise where G : struct, IGradient
{
	public float4 GetNoise4(float4x3 positions, SmallXXHash4 hash)
	{
		LatticeSpan4 x = GetLatticeSpan4(positions.c0);

		var g = default(G);
		return lerp(g.Evaluate(hash.Eat(x.p0), x.g0), g.Evaluate(hash.Eat(x.p1), x.g1), x.t);
	}
}

用同样的方法修改下Lattice2D,使用IGradient.Evaluate函数来替换以前的,传入的晶格点的相对坐标不要写错了.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public struct Lattice2D<G> : INoise where G: struct, IGradient
{
	public float4 GetNoise4(float4x3 positions, SmallXXHash4 hash)
	{
		…

		var g = default(G);
		return lerp(
			lerp(
				g.Evaluate(h0.Eat(z.p0), x.g0, z.g0),
				g.Evaluate(h0.Eat(z.p1), x.g0, z.g1),
				z.t),
			lerp(
				g.Evaluate(h1.Eat(z.p0), x.g1, z.g0),
				g.Evaluate(h1.Eat(z.p1), x.g1, z.g1),
				z.t),
			x.t);
			//) * 2f - 1f;
	}
}

Lattice3D函数也一样.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
public struct Lattice3D<G> : INoise where G : struct, IGradient
{
	public float4 GetNoise4(float4x3 positions, SmallXXHash4 hash)
	{
		…

		var g = default(G);
		return lerp(
			lerp(
				lerp(
					g.Evaluate(h00.Eat(z.p0), x.g0, y.g0, z.g0),
					g.Evaluate(h00.Eat(z.p1), x.g0, y.g0, z.g1),
					z.t),
				lerp(
					g.Evaluate(h01.Eat(z.p0), x.g0, y.g1, z.g0),
					g.Evaluate(h01.Eat(z.p1), x.g0, y.g1, z.g1),
					z.t),
				y.t),
			lerp(
				lerp(
					g.Evaluate(h10.Eat(z.p0), x.g1, y.g0, z.g0),
					g.Evaluate(h10.Eat(z.p1), x.g1, y.g0, z.g1),
					z.t),
				lerp(
					g.Evaluate(h11.Eat(z.p0), x.g1, y.g1, z.g0),
					g.Evaluate(h11.Eat(z.p1), x.g1, y.g1, z.g1),
					z.t),
				y.t),
			x.t);
			//) * 2f - 1f;
	}
}

现在必须在NoiseVisualization中显示地使用Value作为泛型参数.

1
2
3
4
5
6
static ScheduleDelegate[] noiseJobs =
{
	Job<Lattice1D<Value>>.ScheduleParallel,
	Job<Lattice2D<Value>>.ScheduleParallel,
	Job<Lattice3D<Value>>.ScheduleParallel
};

与以前一样,我们现在可以轻松的添加其他类型的梯度噪声了.

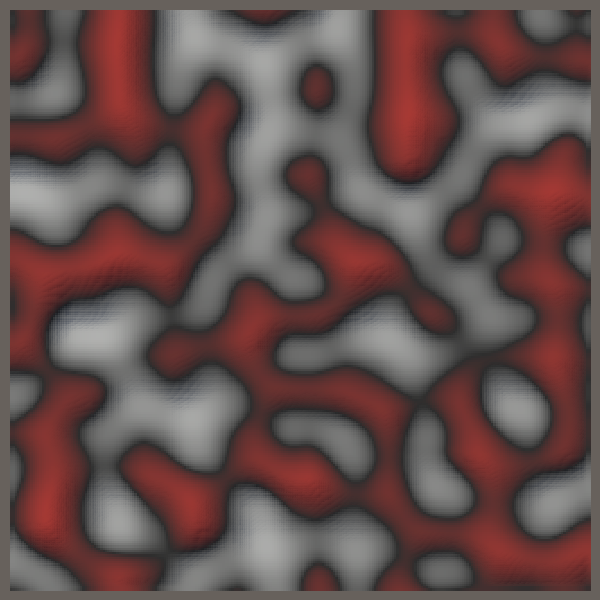
2 柏林噪声(Perlin Noise)

Ken Perlin制作了这种噪声的第一个版本,因此这个经典的噪声被称为**柏林(Perlin)**噪声.与我们目前已经知道的梯度噪声相比,柏林噪声增加了梯度向量可以有不同方向的设计.对这些不同方向的梯度进行插值,可以生成比值噪声更多的变化和更少的块状效果.

柏林噪声不是基于查表计算的吗?

可以,但是查表只是计算方法的其中一种.它能在性能平平的硬件上获得不错的效率,但是域的整体范围会很小,而且不能设定种子.并且这样就不能使用向量化的数组,利用SIMD指令优化计算了.所以我们需要用SmallXXHash4来代替.

2.1 Second Gradient Noise Type

为了实现Perlin噪声,照着写Value那样,在Noise.Gradient中添加一个继承于IGradient的Perlin结构体,先让所有Evaluate返回0.

1
2
3
4
5
6
7
8
public struct Perlin : IGradient
{
	public float4 Evaluate(SmallXXHash4 hash, float4 x) => 0f;

	public float4 Evaluate(SmallXXHash4 hash, float4 x, float4 y) => 0f;

	public float4 Evaluate(SmallXXHash4 hash, float4 x, float4 y, float4 z) => 0f;
}

然后把NoiseVisualization类中的job组数变成2维的.2维数组的元素索引有两部分,所以声明的写法要从ScheduleDelegate[]变成ScheduleDelegate[,].然后将现有的代码写在第二组大括号中,并在值噪声之前加入一组新的柏林噪声的Job参数集合.

1
2
3
4
5
6
7
8
9
10
11
12
13
static ScheduleDelegate[,] noiseJobs =
{
	{
		Job<Lattice1D<Perlin>>.ScheduleParallel,
		Job<Lattice2D<Perlin>>.ScheduleParallel,
		Job<Lattice3D<Perlin>>.ScheduleParallel
	},
	{
		Job<Lattice1D<Value>>.ScheduleParallel,
		Job<Lattice2D<Value>>.ScheduleParallel,
		Job<Lattice3D<Value>>.ScheduleParallel
	}
};

我们添加一个枚举变量来随意切换柏林噪声和值噪声,修改UpdateVisualization的代码,并把这个参数作为组数的第一个参数.

1
2
3
4
5
6
7
8
9
10
11
12
public enum NoiseType { Perlin, Value }

[SerializeField]
NoiseType type;
	
…
	
protected override void UpdateVisualization(NativeArray<float3x4> positions, int resolution, JobHandle handle)
{
	noiseJobs[(int)type, dimensions - 1](positions, noise, seed, domain, resolution, handle).Complete();
	noiseBuffer.SetData(noise);
}

Noise type configuration option.


2.2 1D梯度(1D Gradients)

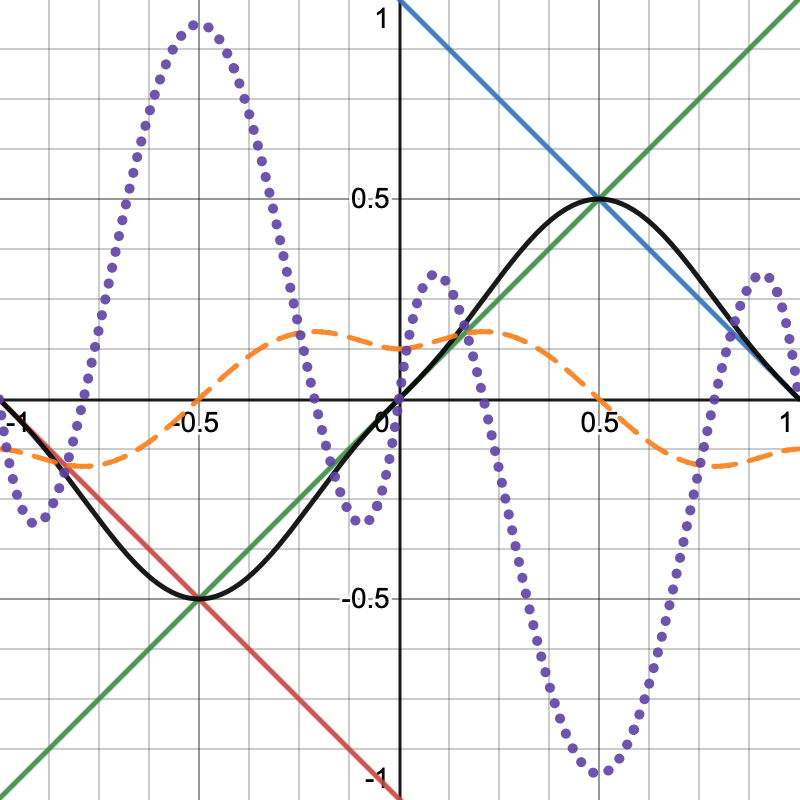
Ken Perlin从没做过一个真正的1D噪声,因为这个基本没用.但是我们做了,因为这对理解更高维度的算法有帮助.我们已经用固定梯度函数$f(x)=x$测试过了1D梯度噪声.柏林噪声认为晶格点的梯度可以是不同的,在1D维度下,另一个不同的最简单的梯度函数,就是上面那个函数的负数版本,即$f(x)=-x$.我们可以使用hash值的第一个bit位来确定要选择正或负的版本.

使用可变梯度时噪声依然是连续的吗?
是的,二阶导数在晶格点的位置始终是0,一阶导数始终是连续的,因为在两端晶格点的梯度是一样的.

Negative-positive-negative gradients, derivatives divided by 8 to fit.
Positive-positive-negative gradients, derivatives divided by 8 to fit.

1
2
3
4
5
public struct Perlin : IGradient
{
	public float4 Evaluate(SmallXXHash4 hash, float4 x) => select(-x, x, ((uint4)hash & 1) == 0);	
	…
}

这导致晶格点之间的跨度有四种插值组合:正-正,负-负,正-负,负-正.由于正和负是镜像的,所以实际只有两种独特的情况:斜率变化相同和不同.

1
public float4 Evaluate(SmallXXHash4 hash, float4 x) => 2f * select(-x, x, ((uint4)hash & 1) == 0);

1D binary Perlin noise; domains scale 16; resolution 256.

2.3 可变型梯度算法(Variable Gradients)

我把上面做出来的那种噪声命名为二分(binary)柏林噪声,因为它的梯度只能有两种状态.噪声由一连串指向同一方向的梯度序列组成,只是会有上下波动.整个序列看起来有小部分大振幅的波形,而其余的是小振幅波型.不过这看起来非常僵硬,让我们试试不同的方法.

与其二分选择,不如用一个转换到[-1,1]之间的hash值作为因子来缩放相对坐标.不过仍需要翻倍计算结果使最大振幅为1.

1
public float4 Evaluate(SmallXXHash4 hash, float4 x) => 2f * (hash.Floats01A * 2f - 1f) * x;

Variable gradients.

这效果看上去就更加有趣了,我们得到了一个有更多不同振幅的梯度效果.当然这让达到最大振幅的可能性降低了,因为序列的平均振幅降低了.

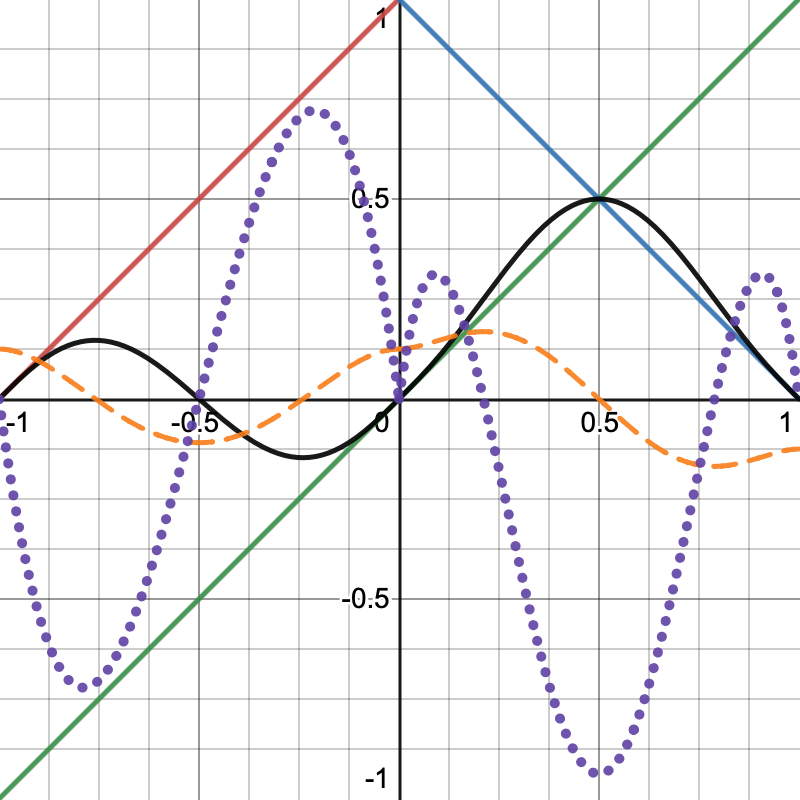
我们还可以组合可变和二分两个算法,使用hash第1个bit位来选择正负,并乘以Floats01A作为系数.

1
public float4 Evaluate(SmallXXHash4 hash, float4 x) => 2f * hash.Floats01A * select(-x, x, ((uint4)hash & 1) == 0);

不过这样写会让第1bit位被使用两次,为了避免这种情况,我们使用第9bit位来确定正负.

1
2f * hash.Floats01A * select(-x, x, ((uint4)hash & 1 << 8) == 0);

Different variable gradients.

这种方法的好处是,无论梯度的方向如何,都有最小振幅,可以防止出现简化的(degenerate areas)区域,在这种区域里面,多个连续的晶格点之间的变化率几乎为0,于是就会出现一段非常平坦的区域.

最简单的方法就是把最小振幅设置为1,然后在这个基础之上加上hash的浮点值,得到的结果可以被当成是混合了二分和可变的两种方法,既保留了最小的振幅,也出现了很多的变化.

1
public float4 Evaluate(SmallXXHash4 hash, float4 x) => (1f + hash.Floats01A) * select(-x, x, ((uint4)hash & 1 << 8) == 0);

Binary-variable mix.

2.4 2D梯度(2D Gradients)

接下来是2D的噪声,我们还是从单个维度的二分梯度算法开始,使用第1bit位计算,看看效果如何.

1
public float4 Evaluate(SmallXXHash4 hash, float4 x, float4 y) => select(-x, x, ((uint4)hash & 1) == 0);

2D binary Perlin noise plane; domain scale 8; top-down view.

结果是带状的1D二分插值图案的平面集合.让我们再一次使用floatA这个方法来重新计算,使梯度更加多样化.

1
public float4 Evaluate(SmallXXHash4 hash, float4 x, float4 y) => (hash.Floats01A * 2f - 1f) * x;

Variable gradients along X.

在2D噪声的中,我们不再被限制于轴对称的梯度,梯度向量可以旋转360度.为了生成这样一个向量,可以使用一种类似于生成八面体球体的方法,但需要减少到二维.

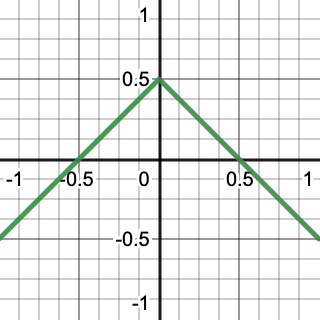
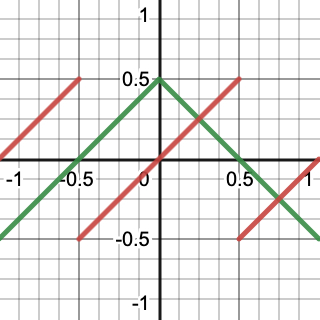
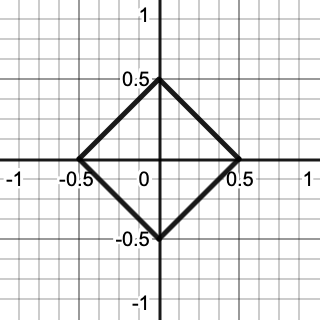
我们从X轴上的一条[-1,1]之间的直线开始,然后令Y等于0.5减去X的绝对值,就像我们在创建八面体的前半部分定义Z轴一样,只是现在少了一个维度.于是就形成了一个楔形,相当于是一个开了口的正方形.然后用X减去floor(X+0.5)来处理正方形的负值部分,使其闭合.

1 2 3

The process of creating a square from a line.

结果就形成了一个四个角挂在X和Y轴上的正方形,每个角都距离原点0.5个单位.梯度向量就从原点指向正方形的边上的某点.

为了计算二维的梯度,我们将其X和Y分量相加.最后翻倍这个值使轴对称向量的长度等于1.

1
2
3
4
5
6
7
public float4 Evaluate(SmallXXHash4 hash, float4 x, float4 y)
{
	float4 gx = hash.Floats01A * 2f - 1f;
	float4 gy = 0.5f - abs(gx);
	gx -= floor(gx + 0.5f);
	return (gx * x + gy * y) * 2f;
}

Square-based gradients.

如果我们想把正方形的分布变成一个圆形分布,可以通过除以它们的长度来对梯度向量进行标准化.但是需要注意的是,这样做并不会产生均匀的圆形梯度分布,因为它们是沿着正方形均匀分布的,所以更集中于正方形的四个角附近,就像正八面体球体更集中在6个角上一样.不过这并没有什么问题,因为分布是对称的,而且有足够多的变化.

1
return (gx * x + gy * y) * rsqrt(gx * gx + gy * gy);

Normalized gradients.

然而这对于最终效果来说,并不会产生很大的不同,所以我们可以省略掉这一部分,还能让代码跑的更快.标准化确实对对角型梯度更有利,但是噪声本身也需要标准化,我们后续可以解决这个问题.

1
return (gx * x + gy * y) * 2f;

2.5 标准化2D噪声(Normalized 2D Noise)

为了标准化噪声,我们需要找到最大的振幅.如果一个晶格方形有4个都指向中心的梯度,那么最大值将处在中心点的位置.因为这点是四个相等梯度的平均值,所以我们只需要计算位于此点的单个梯度的值.一个完美的对角型梯度函数是$f(x,y)=\frac{x+y}{2}$,所以中心点的振幅就是$f(0.5,0.5)=\frac{1}{2}$.不过这并不是最大的振幅,因为还有一种配置的梯度算法可以得到更大的振幅.

当两个梯度都在同一个轴上相互直指向对方,此时将处于晶格跨度正中间,这就是单个维度上的最大值0.5.这是没有被标准化的1D二分柏林噪声.如果晶格方形的另一边的两个梯度直指它们对面的这两个晶格点,那么在两个维度上进行插值计算之后,在某点上可以算出来一个超过0.5的值.

Gradients for maximum amplitude.

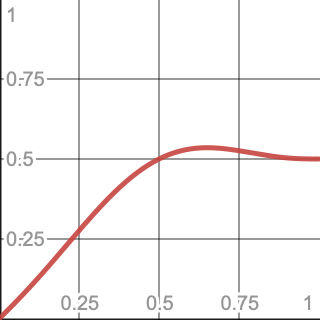
因为最大值是由一维中点沿着第二个维度上进行插的某点,所以这本质就是一个在轴对称梯度和0.5之间进行平滑差值的函数.因此我们必须找到当$s(t)=6t^5−15t^4+10t^3$时,函数$xs(1−x)+0.5s(x)$在范围[0,1]之间的最大值.

把这个函数展开得到$6x(1-x)^5-15x(1−x)^4+10x(1−x)^3+3x^5−7.5x^4+5x^3$.

然后可以简化成$−6x^6+18x^5−17.5x^4+5x^3+x$.

为了找到最大值,我们必须对函数求导来寻找0这组解,因为当变化率为0时,原函数此时就达到最大值或最小值.这个值可以被算出来,但只靠硬算很难.所以为了知道函数长成什么样,我们可以使用Desmos将其可视化.通过选择这条函数曲线上的某一点,我们可以立即得知,当X坐标位于0.6509处时,最大值为0.5353,它的确大于0.5.

2D maximum graph.

我们问问专业的Wolfram|Alpha,让它告诉我们一个更精确的最大值.专业网站给了我们一个超级精确的答案,但它太变态了,所以我们用近似值0.53528来代替就行了.比起Desmos来说,这个答案精确到了后一位.于是,将梯度除以这个值,就能得到归一化的2D柏林噪声.

1
return (gx * x + gy * y) * (2f / 0.53528f);

1
2

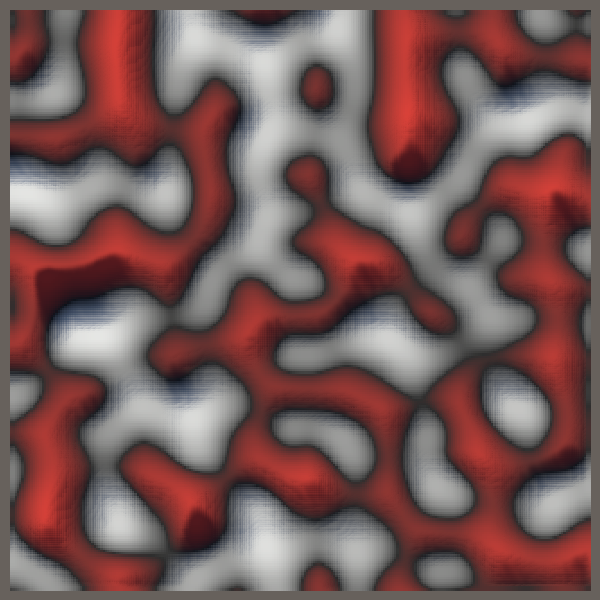
Normalized 2D Perlin noise.

圆形梯度的最大振幅是多少?

完美对角型梯度的圆形版本的函数是$f(x,y)=\frac{x+y}{\sqrt{2}}$.所以最大振幅,是在所有梯度都指向晶格块中心时,这个函数为$f(0.5,0.5)=\frac{1}{\sqrt{2}}\approx0.7071$.因此为了标准化噪声,我们必须除以这个数,或者乘以$\sqrt{2}\approx1.4142$.

2.6 3D梯度(3D Gradients)

为了创建3D柏林噪声,我们得像做2D噪声那样,不过要扩大一维.这里同样可以使用生成八面体的方法.在这种情况下,我们就需要两个在[−1,1]范围内的随机值.我们将使用Floats01A和Floats01D.D算法快于B或C算法,因为单比特的移位操作,比移位操作加模操作要快.

1
2
3
4
5
6
7
8
9
public float4 Evaluate (SmallXXHash4 hash, float4 x, float4 y, float4 z)
{
	float4 gx = hash.Floats01A * 2f - 1f, gy = hash.Floats01D * 2f - 1f;
	float4 gz = 1f - abs(gx) - abs(gy);
	float4 offset = max(-gz, 0f);
	gx += select(-offset, offset, gx < 0f);
	gy += select(-offset, offset, gy < 0f);
	return (gx * x + gy * y + gz * z);
}
3D柏林噪声不是只需要使用12个梯度向量吗?

柏林噪声的参考实现的确是这样的,从一组12个不同方向的2D对角梯度向量,指向立方体边缘中心,然后经过一些重复,最终会得到16个选项.于是,四个比特的值就可以转换为梯度.虽然这种方法对于普通编码方式或专用硬件来说是挺不错的,但嵌套型的二分函数代码并不能利用SIMD指令加速.我们这种基于八面体的方法既快(如果我们不对梯度进行归一化计算),又能提供更多的花样.

就跟找2D最大振幅一样,把梯度沿着第三个维度进行插值,此梯度沿着当前维度的轴向指向对面2D晶格平面,直到移动到最大值0.53528处.接下来像处理2D晶格方形的函数那样,要最大化函数的值,用0.53528替换0.5:$xs(1−x)+0.53528s(x)$,此函数可以展开成$6x(1−x)^5−15x(1−x)^4+10x(1−x)^3+0.53528(6x^5−15x^4+10x^3)$,输入Desmos后可以得到X在0.6732时最大,结果等于0.5629.

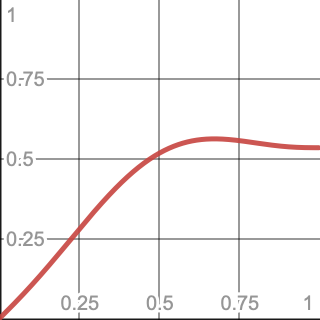
3D maximum graph.

Wolfram|Alpha说在0.67321时的值是0.56290.

1
return (gx * x + gy * y + gz * z) * (1f / 0.56290f);

Octahedron-based 3D Perlin noise.

3D球体梯度的最大振幅是多少?

为了用球体梯度向量代替八面体,梯度向量要直指晶格体的中心,即函数$f(x,y,z)=\frac{x+y+z}{\sqrt{3}}$.所以最大振幅值可以在晶格体的中心位置找到,即$f(0.5,0.5,0.5)=\frac{1.5}{\sqrt{3}}\approx0.8660$.除以这个值就可以标准化噪声了.


原文授权协议


原文项目仓库地址

我写的单CPU端萌新入坑版项目地址

伪随机算法系列-04 Perlin Noise(Gradient Noise)

https://tzkt623.github.io/2022/01/14/Pseudorandom Noise-04 Perlin Noise/

作者

特兹卡特(Tezcat)

发布于

2022-01-14

更新于

2022-01-20

许可协议

#

觉得还不错,请我喝杯饮料吧!

Bilibili

分类

归档

标签

C++1
Coordinate1
Noise5
Pseudorandom5
Random5
Scale1
Unity6
regex1
正则表达式1

最新文章

×